Задания по геометрии

Решение:

                             K                                      M

 

                                            C

                          P                                          N

 

     Треугольник MCN равнобедренный, так как диагонали прямоугольника равны между собой и в точке пересечения делятся пополам. Углы при основании равнобедренного треугольника между собой равны, а сумма всех углов треугольника равна 180 градусов. Получаем:

 Ð MCN + Ð MNC + Ð NMC = 180° Ð MNC  = Ð NMC

 2ÐMNC + 46° = 180°. 

ÐMNC = (180° - 46°):2

ÐMNC = 67°

Верный ответ 1)

 

 

 

 

                                         A                                                                                B

 

 

 

 

                                              O

                     M

 

 

 

Решение: ОА – радиус окружности, АВ – касательная к окружности. Значит OA ^ AB. Треугольник OAB прямоугольный с прямым углом BAO. Ð AOB = 60°,  Ð ABO = 30°. Катет прямоугольного треугольника AO лежит против угла в 30°, значит  длина AO  равна половине гипотенузы. R = AO = 0,5OB = 0,5×8 = 4.

Верный ответ 4)

 

 

 

 

 

 

                                        B

 

 

 

 

 

 

               A                                     C                        D

 

Решение: Треугольник АВС по условию равнобедренный. Значит Ð ВАС = Ð АСВ как углы при основании равнобедренного треугольника. ÐВАС = 140° - внешний угол при основании треугольника. Ð АСВ = 180° - 140° = 40°, как угол смежный к внешнему углу. Сумма всех углов треугольника 180°. Получаем Ð АСВ + Ð АСВ + ÐАВС = 180°. Отсюда получаем Ð АВС = 180°- 80° = 100°.

Верный ответ 2).

 

 

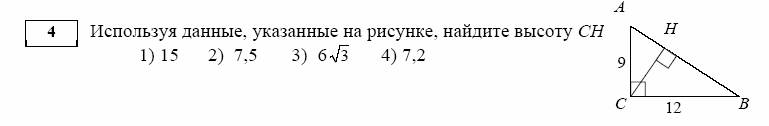
Решение: В прямоугольном треугольнике высота CH² = AH×HB, катеты: AC² = AH×AB, CB² = BH×AB. AB² = AC² + BC² => AB² = 81+144 = 225 => AB = 15. AC² = AH×AB = 81 = AH×15 => AH = 5,4. CH² = AC² – AH² => CH² = 81 – 29,16 = 51,84 => CH = 7,2

Верный ответ 4).

Решение: Из формулы длины окружности C = 2pr.

Записать ответ: 14,5

 

Решение: Треугольник ABO подобен треугольнику COD, потому что Ð ABO = ÐODC при параллельных прямых АВ и CD и секущей BD. ÐBOA = ÐCOD – как вертикальные. У подобных треугольников соответствующие стороны пропорциональны. Значит получим: AB:AO = DC:CO => 6:10 = 9:OC => OC = 15, AC = AO + OC = 10 + 15 = 25.

Записать ответ 25.

 

 

 

 

 

        A              K                      L        B

 

 

 

 

 

                   D                            C

Решение: Трапеция равнобедренная, значит AD = BC, Основания DC и  AB параллельны, значит высоты равны: DK = CL. Треугольники ADK и BLC равны (прямоугольные равные по катету и гипотенузе). Значит   AK = LB. KL = DC – противоположные стороны прямоугольника DKLC. Получаем LB = (AB – DC):2 = (19 – 9 ) :2 = 5. В прямоугольном треугольнике CLB необходимо найти гипотенузу CB(боковая сторона трапеции). По теореме Пифагора CB² = LB²+LC². => CB²=25 + 144 = 169 => CB = 13.

Записать ответ 13.

 

 

 

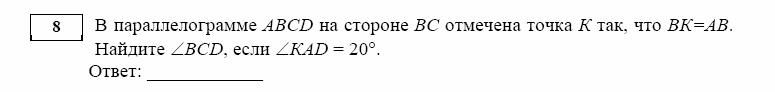
                           D                                        C      L

                                                               K

 

                  

 

 

 

 

        A                                              B

 

Решение: треугольник ABK -  равнобедренный, так как BK = BA. Значит Ð ВАК = ÐАКВ, a ÐАКВ = Ð KAD (внутренние накрест лежащие при параллельных AD, BC и секущей AK). ÐBCD = ÐDAB =  Ð KAD + Ð ВАК = Ð KAD + Ð KAD = 20°+ 20° =40°.

Записать ответ 40.

                Ответ…………………….

Решение: В равностороннем треугольнике все углы по 60°. Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними. Получаем: LM×LN = 6×6×cos60° = 36×0,5 = 18.

Записать ответ 18.

Решение: В правильном двенадцатиугольнике  А₁А₅ = А₅А₉ = А₉А₁. Значит радиус окружности описанной около правильного двенадцатиугольника будет и радиусом окружности описанной около правильного треугольника А₁А₅А₉. Формула стороны правильного многоугольника через радиус описанной окружности a_n = 2Rsin180/n => a₃ = 2×  sin60° = 10×   = 15.

Записать ответ 15.

 

Решение: Площадь всего листа фанеры равна 10дм×5дм = 50дм². Из полной площади необходимо вычесть площадь двух равнобедренных треугольников. Площадь треугольника равна половине произведения основания на высоту. Длина основания равна ширине прямоугольника, т.е. 5дм, а высота (10 – АВ):2 = (10 – 6):2 = 2. Тогда площадь двух треугольников будет равна 5дм×2дм=10дм²

Найдём поверхность, которую нужно закрасить 50дм² – 10дм²  = 40дм². Определяем массу краски – 40×0,012 = 0,48

Записать ответ 0,48

Решение:

1) утверждение ложное, у квадрата углы прямые. 2) утверждение верное. 3) Утверждение верное – квадрат является ромбом. 4) Утверждение неверное, диаметр окружности вписанной в квадрат равен стороне квадрата. 5) утверждение верное a₄ = 2Rsin45° = RÖ2.

Записать ответ 235.