Демонстрационный вариант ЕГЭ 2009 по алгебре в 9 классе

Часть I

 

1

 Расположите в порядке возрастания числа: 0,0902; 0,09; 0,209.

1) 0,209; 0,0902; 0,09      2) 0,09; 0,0902; 0,209     3) 0,09; 0,209; 0,0902         4) 0,0902; 0,09; 0,209

Решение: Сравниваем целые части, они равны, сравниваем десятичные, у первых двух равны, а у третьего числа 2, значит оно наибольшее. Аналогично сравниваем 0,0902 и 0,09, выбираем большее 0,0902. Тогда по возрастанию получим 0,09; 0,0902; 0,209.

Верный ответ 2).    

2

Какое из чисел , ,  является рациональным?

1)                        2)              3)                 4) ни одно из этих чисел

Решение: -  не рациональное,  - не рациональное,  = 20 – рациональное.

Верный ответ 3)

 

3

Дневная норма потребления витамина С составляет 60 мг. Один мандарин
в среднем содержит 35 мг витамина С. Сколько (приблизительно)
процентов дневной нормы витамина С получил человек, съевший один
мандарин?
1) 170%                        2) 58%                           3) 17%                         4) 5,8%

Решение: Необходимо определить, сколько процентов составляет 35 от 60.

35:60×100% = 58,(3)

 

Верный ответ 2)

 

4

Найдите значение выражения  при а = 8,4; b = –1,2; с = – 4,5.

Решение: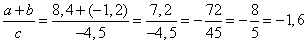

Записать в ответ – 1,6.

 

5

Один килограмм орехов стоит a рублей. Составьте выражение для

вычисления стоимости n грамм этих орехов (в рублях).

1) 1000аn                  2) an                       3)                      4)

Решение: Один килограмм орехов стоит a рублей, n килограммов стоит an, то n грамм в 1000 раз меньше.

Верный ответ 3)

 

6

В каком случае выражение преобразовано в тождественно равное?

 

1) 3(x – y) = 3x – y  2) (3 + x)(x – 3) = 9 – x² 3) (x – y)² = x² – y²  4) (x + 3)² = x² + 6x + 9

 

Решение: 1) 3(x – y) = 3x – 3y – распределительное свойство, 2) (3 + x)(x – 3) = x² – 9 – разность квадратов, 3) (x – y)² = x² – 2xy + y² – квадрат разности, 4) (x + 3)² = x² + 6x + 9 – квадрат суммы.

Верный ответ 4)

7

 

Упростите выражение .

1)                 2)                           3)                            4)

 

Решение:

Верный ответ 4)

 

8

Упростите частное . Ответ запишите в виде десятичной дроби

Решение: 

Записать ответ 0,012.

 

9

Решите уравнение 3 – 2x = 6 – 4(x + 2).

Решение

3 – 2x = 6 – 4(x + 2).

3 – 2x = 6 – 4x – 8

      – 2x + 4x = 6 – 3 – 8

              2x = – 5

                    x =– 2,5

Записать ответ –2,5.

 

 

10

Прямая y = 2x пересекает параболу y = -x² + 8 в двух точках. Вычислите координаты точки A.

 

Решение:

Для нахождения точек пересечения прямой и параболы необходимо решить систему уравнений  Решаем методом подстановки  

Находим корни уравнения по теореме Виета. Произведение корней – 8, сумма – 2. Тогда корни: x₁ = – 4 x₂ = 2. Найдём значения ординат y₁ = 2(- 4) = - 8, y₂ = 2×2 = 4. Тогда точки пересечения  B(-4; -8), A(2; 4).

Верный ответ A(2; 4).

 

11

Прочитайте задачу: «Периметр прямоугольника равен 20 см. Длины его

смежных сторон относятся как 3 : 2. Найдите длины сторон этого

прямоугольника.»

Пусть a и b – длины сторон прямоугольника (в см), причем, a — длина большей

стороны. Какая система уравнений не соответствует условию задачи?

 1)              2)           3)                   4)                                

Решение: Периметр P = 2(a + b), Составим пропорцию a:b = 3:2, т.к. a > b.

P = 20. Получим 2(a + b) = 20 и a:b = 3:2 , соответствует 1), 2), 3)

Верный ответ 4).

12

Решите неравенство 10x – 4(2x – 3) > 4.

1)             2) x > 8           3) x > -4                   4) x < -4

 

Решение: 10x – 4(2x – 3) > 4

                 10x – 8x + 12 > 4

                         2x > - 8

                          x > - 4

Верный ответ 3)

 

13

        На рисунке изображён график функции y = x² + 2x.     

        Используя график, решите неравенство x² + 2x > 0.

 

        1) (-∞; 0)     2) (-∞;  - 2)È (0; +∞)   3)(-2; 0)   4) (-2; +∞) 

 

Решение: x² + 2x > 0, х соответствует решению неравенства там где ветви параболы выше оси ОХ, а это соответствует  2)

Верный ответ 2)

14

Для каждой арифметической прогрессии, заданной

формулой n-го члена, укажите ее разность d. (В таблице под каждой

буквой запишите номер ответа, под которым указана соответствующая

разность.)

A) a_n = 7n + 5                   Б) b_n = 10n + 7                           В) с_n = 5n – 10

1) d = -10                2) d = 7                  3) d = 5                  4) d = 10

Решение: Формула n – го члена имеет вид a_n = a₁ + d(n – 1)

A) a_n = 7n + 5 = 7(n – 1) + 12  d = 7

Б) b_n = 10n + 7 = 10(n – 1) +17 d = 10

В) с_n = 5n – 10 =5(n – 1) -5  d = 5

 

Ответ:

А)	Б)	В)
2	4	3

      

 

 

15

График какой квадратичной функции изображён на рисунке?

 

 

1) y = x² + 4x – 5                                 2) y = -x² - 6x – 5

3) y = x² - 4x – 5                                 4) y = -x² + 6x – 5

            

Решение: Найдём точки пересечения графиков с осью ОХ, т.е.

решим уравнения: x² + 4x – 5 = 0, x² - 4x – 5 = 0.

x² + 4x – 5 = 0 – корни – 5 и 1 пересекает в точках (-5; 0) и (1; 0) –

 ветви графика вверх е. к. первый коэффициент больше нуля.

x² - 4x – 5 = 0 – корни 5 и – 1 пересекает в точках (-1; 0) и (5; 0) -

ветви графика вверх е. к. первый коэффициент больше нуля.

Графики y = -x² - 6x – 5 и y = -x² + 6x – 5 направлены ветвями вниз.

Верный ответ 3)

 

 

 

 

 

16

 

 

Фирма «Связь» выпустила в продажу две новые модели телефонов — модель А и

модель В. На графиках показано, как эти модели продавались в течение года. (По горизонтальной оси откладывается время, прошедшее с начала продаж, в месяцах; по вертикальной — число телефонов, проданных за это время, в тыс. шт.) Сколько всего телефонов этих двух моделей было продано за первые десять месяцев?

 

Решение: Моделей типа А за 10 месяцев продано 400 тыс.Моделей типа В за 10 месяцев продано 400 тыс. Всего 800 тыс.

Записать ответ 800 тыс.

Часть II

Задание 17

Постройте график функции  . Укажите наименьшее значение этой функции.

Задание 18

Выясните, имеет ли корни уравнение x² +2x + 2x = - 11.

 

Задание 19

Найдите сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.

Задание 20

Найдите наименьшее значение выражения (2x + y +3)² + (3x – 2y + 8)² и значения x и y, при которых оно достигается.

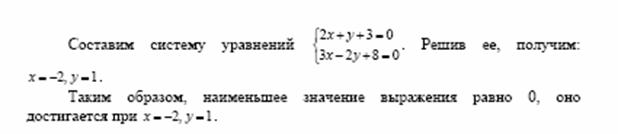
Задание 21

Найдите все значения k, при которых прямая y = kx пересекает в трёх различных точках ломаную, заданную условиями: